Introduction
This article is part of the data structure category
A stack is an abstract data structure defined by its behavior rather than its implementation details. It’s also dynamic, meaning it can adjust its size once created.
A stack implements a method of handling elements named LIFO, last-in first-out, where the last inserted element in the stack is going to be the first one to be picked up; this design makes the usage of this data structure excellent for use cases, for example, as “undo/redo” (AKA ctrl+z/ctrl+y).

Implementation
Since a stack is an abstract data structure, in this article, the underlying implementation of it will be a singly linked list.
Also, at the end of the article, there will be a small implementation of a stack using a slice (dynamic sized array).
It is worth mentioning that even if the behaviors are the same, the stack’s time and space complexity using a singly is more efficient than the slice one; you can find the details in the related section.
The implementation of a stack in this article is a type named Stack, which has three fields:
- head: a pointer to the first element of the stack; when null, it means there are no elements at all.
- length: to keep track of how many elements the stack is storing without traversing the whole sequence.
- mutex: to ensure that the singly is thread-safe.
In Go, an implementation may look like this:
type Stack struct {
mu sync.Mutex
head *node
len uint
}
Along with the Stack type, it is mandatory to create a node type as well, which has two fields:
- val: the value stored in the stack
- next: a pointer to the next element; when null, it means there are no other elements
type node struct {
val interface{}
next *node
}
In this implementation, the node allows storing any data type, thanks to an empty interface contract.
A stack has two main behaviors:
- Push: add an element at the top of the stack
- Pop: get an element from the top of the stack
Push
Pushing an element into a stack can be a cheap operation depending on the technical implementation. It is possible to shape this data structure not to traverse any of the elements it contains.

Some elements need to be pushed into an empty stack.
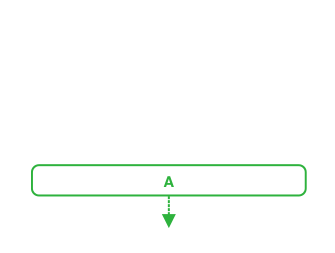
To push an element into a stack when it is empty, place it at the first available position, which is the stack's bottom.
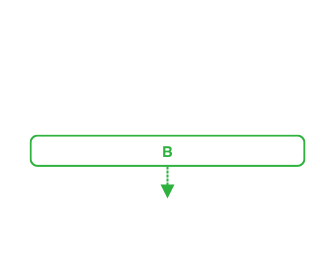
Similarly, to add an element into a non-empty stack, place the new element before the last added one, which is A in this case.
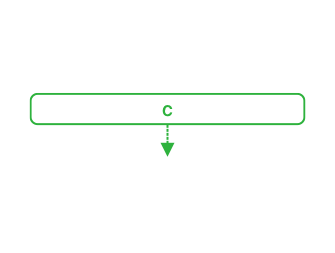
It is essential to mention that a stack can grow (virtually) infinitely, meaning it is possible to push as many elements as needed in the stack.

Since this is an abstract data type, the time complexity of pushing an element into the stack depends on the implementation details. Still, it is possible to achieve an O(1) time complexity.
A simple Go method can implement this behavior:
func (s *Stack) Push(v interface{}) {
// lock meanwhile the operation is ongoing
s.mu.Lock()
defer s.mu.Unlock()
// increase the internal counter of nodes
s.len++
// add the new node as top one, and shift the previous one in the second position
s.head = &node{val: v, next: s.head}
}
Pop
Popping an element from a stack can be a cheap operation for the same reason as the pushing method.
The main difference between the Push, and the Pop behavior is that the Pop one should fail when the stack is empty, returning an error or using the “comma ok” idiom.

Some elements need to be popped from a stack already containing two elements.
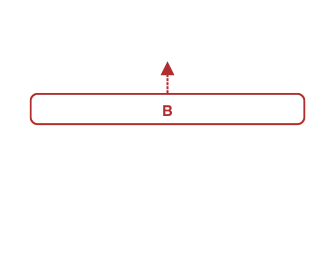
To pop an element from a stack, pick the element at the top position, and remove it from the top before giving it to the caller.
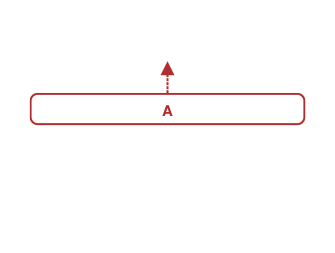
Similar to the first pop operation, to remove the last element from a stack, pick the last element and remove it from the stack, which is A in this case.
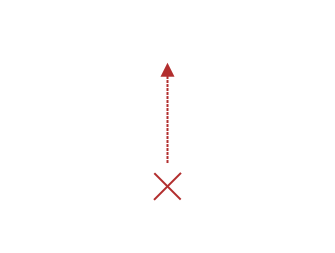
When popping from an empty stack, it is mandatory to communicate to the caller that no element has been popped out.

Since this is an abstract data type, the time complexity of popping an element from a stack, it's coupled with its implementation details, but it is possible to achieve an O(1) time complexity.
This behavior can be written down in some Go code looking like this:
func (s *Stack) Pop() (interface{}, bool) {
// lock meanwhile the operation is ongoing
s.mu.Lock()
defer s.mu.Unlock()
// if there are no node return false to notify that the operation did not pop any node
if s.head == nil {
return nil, false
}
// decrease the internal counter of nodes
s.len--
// read the value from the top node
v := s.head.val
// remove the previous head from the stack
s.head = s.head.next
// return the found value and true to notify that the operation pop a node
return v, true
}
An alternative
As mentioned at the beginning, this is an implementation of a stack data structure using a slice.
This implementation is less efficient than using the singly linked list one since in both the methods Push and Pop we need to shift all the slice items, increasing the time complexity from an O(1) to an O(N).
Note: it is possible to achieve an O(1) complexity on the Pop operation if the implementation would insert the data at the bottom of the slice
type Stack []interface{}
func (s *Stack) Push(v interface{}) {
*s = append([]interface{}{v}, *s...)
}
func (s *Stack) Pop() (interface{}, bool) {
if len(*s) == 0 {
return nil, false
}
var v interface{}
v, *s = (*s)[0], (*s)[1:]
return v, true
}
func (s *Stack) Len() uint {
return uint(len(*s))
}
Conclusion
The stack data structure is quite simple to implement; even doing it in a way that is efficient for both time and space complexity ends up with a simple implementation.
It is also possible to implement methods, such as Search, but those are not part of a standard stack definition; please, keep the data structure small and straightforward, and avoid adding other behavior pushing to misuse it.
To end the article, here is a recap of the time complexity of the operations a stack can support:
| Operation | Time complexity |
|---|---|
| Push | O(1) |
| Pop | O(1) |