Introduction
This article is part of the data structure category
A linked list is a linear data structure formed by a collection of sequential elements.
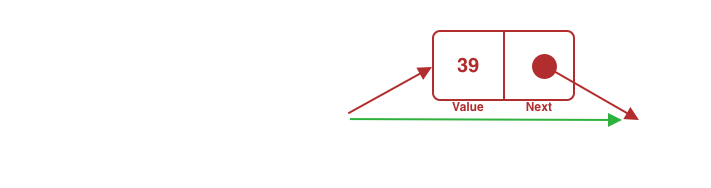
In the linked list, an element is a node that stores a value and, depending on the implementation, one or more link to the next elements.
This detail makes the linked list a dynamic data structure, which means it can grow or shrink its size.
The singly linked list is an implementation of a linked list where each node holds a single link to the next one whenever it is present, meaning that a program can traverse a linked list only one way.
Implementation
The implementation of the singly linked list for this article is a type named Singly, which has three fields:
- head: a pointer to the first node of the singly, when null it means there are no nodes at all.
- length: to keep track of how many nodes the singly is storing without traversing the whole sequence.
- mutex: to ensure that the singly is thread-safe.
Some singly implementation may also have a tail field, which reduces the cost of insertion/deletion to the end of the linked list, but this will not be the case.
In Go, an implementation may look like this:
type Singly struct {
mu sync.Mutex
len uint
head *singlyNode
}
Along with the Singly type, it is mandatory to create a singlyNode type as well, which has two fields:
- value: the value stored in the singly
- next: a pointer to the next node; when null, it means there are no other nodes
type singlyNode struct {
value interface{}
next *singlyNode
}
In this implementation the node allows storing any data type, thanks to an empty interface contract.
Let’s go through the behavior a linked list usually has.
Add
Adding a node into a singly can be a cheap or an expensive operation, depending on which position it needs to add the new node.
Adding in front
A third node needs to be added at the beginning of a singly with two nodes.
Select the head node of the singly.
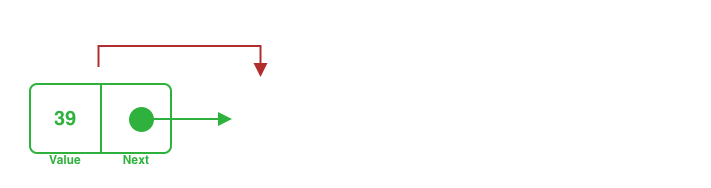
Designate the new node as the new head and point it to the previous one to maintain the sequence's integrity.
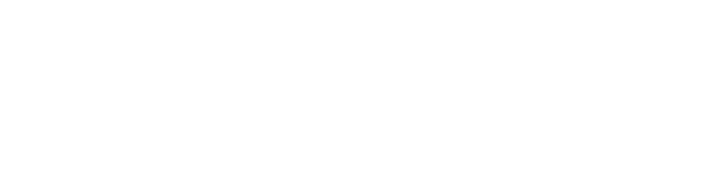
Since there is no need to traverse the singly except accessing the head node, the time complexity for this operation is a O(1).
It is possible to implement this behavior by adding a simple function (method in Go) similar to this:
func (s *Singly) AddFront(v interface{}) {
// lock while the operation is ongoing
s.mu.Lock()
defer s.mu.Unlock()
// increase the internal counter of nodes
s.len++
// set the new node at the head and the previous one as next
s.head = &singlyNode{value: v, next: s.head}
}
Adding to the back
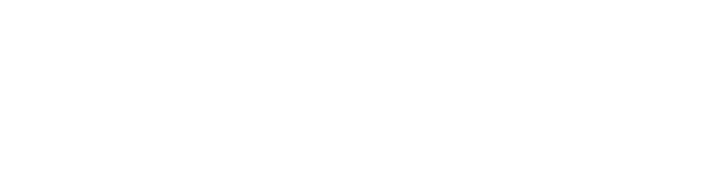
A third node needs to be added to the end of a singly with two nodes
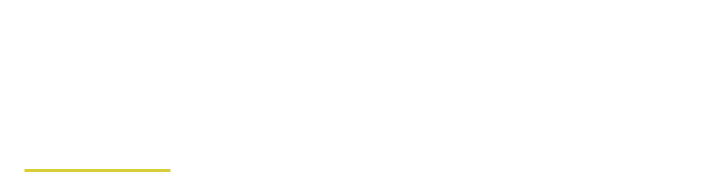
Keep moving ahead in the sequence as long as the node is not the last one.
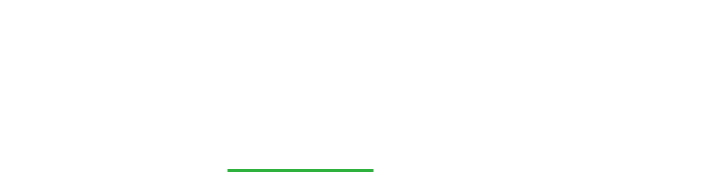
Stop traversing the singly when the currently last node is found.
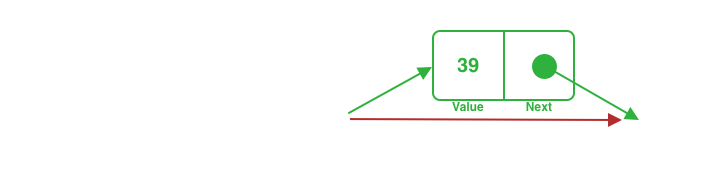
Link the last found node to the incoming node. As the incoming node points it nothing, it will become the new last node.
Since all the singly nodes are going to be traversed, the time complexity for this operation is a O(n).
It is possible to implement the described behavior by adding a function (again, a method in Go) similar to the following one:
func (s *Singly) AddBack(v interface{}) {
// lock while the operation is ongoing
// and increase the counter once the function finished
s.mu.Lock()
defer func() {
s.len++
s.mu.Unlock()
}()
// if there is no head add the first node as such
if s.head == nil {
s.head = &singlyNode{value: v, next: nil}
return
}
// as long as `n` is not the last node, proceed moving ahead in the sequence
n := s.head
for i := s.len; i > 1; i-- {
n = n.next
}
// add the new node as the last in the sequence
n.next = &singlyNode{value: v, next: nil}
}
Delete
Deleting a node from a singly has similar complexity to the add operation.
In fact, the position of the node directly influences the time complexity of it.
Deleting from front
A node needs to be deleted at the beginning of a singly with three nodes.
Select the head node of the singly.
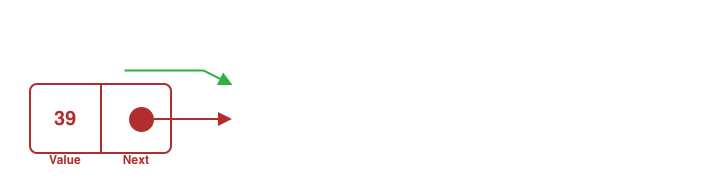
Designate the node next to the selected one as the new head and freely drop the former head node.
Since there is no need to traverse the singly except accessing the head node, this operation's time complexity is an O(1).
It is possible to implement this behavior by adding a simple function (method in Go) similar to this:
func (s *Singly) DeleteFront() bool {
// lock while the operation is ongoing
s.mu.Lock()
defer s.mu.Unlock()
// if there are no items return false to notify that no node was deleted
if s.head == nil {
return false
}
// replace the head with its next item
// and return true to notify a node has been removed
s.len--
s.head = s.head.next
return true
}
Deleting from the back
A node needs to be deleted at the end of a singly with three nodes.
Start traversing the singly from the first node, and keep moving ahead in the sequence as long as the node is not the second to last.
Stop traversing the singly when the second-to-last node is found.
The found node needs to link to nothing, excluding the last node from the singly sequence.
Since all the singly nodes are going to be traversed, the time complexity for this operation is a O(n).
func (s *Singly) DeleteBack() bool {
// lock while the operation is ongoing.
s.mu.Lock()
defer s.mu.Unlock()
// if there are no items return false to mark the did not delete any node.
if s.len == 0 {
return false
}
// decrease the counter once the function return.
defer func() { s.len-- }()
// if there's only the head, delete the not at that position
// and return true to notify a node has been removed.
if s.len == 1 {
s.head = nil
return true
}
// as long as `n` is not the second last node, keep moving ahead in the sequence.
n := s.head
for i := s.len; i > 1; i-- {
n = n.next
}
// delete the last node and return true to notify a node has been removed.
n.next = nil
return true
}
Find
Searching for a value inside a singly is the last behavior I am going to share in this article.
Finding a value in a singly will end in one of two ways; an index of the node holding the given value is found, or the singly doesn’t find a node holding the given value.
Found
A node index needs to be given back if one of the nodes in the singly has that value.
Start traversing the singly from the first node, and keep moving ahead in the sequence as long as the node does not have the given value.
Since the last node in the singly may be the one with the given value, the time complexity for this operation is a O(n).
Not found

A node index needs to be given back if one of the nodes in the singly has that value.

Start traversing the singly from the first node, and keep moving ahead in the sequence as long as the node does not have the given value.
When the position is one the last node, means the value has not been found.
Since all the singly nodes are going to be traversed, the time complexity for this operation is a O(n).
func (s *Singly) Find(v interface{}) (int, bool) {
n := s.head
for i := 0; i < int(s.len); i++ {
switch {
// if `n` is nil, it means there are no more nodes in the singly.
// return 0 and false to notify there is no index matching the value.
case n == nil:
return 0, false
// if the value is matched, then return the index
// and true to mark the success of the operation.
case n.value == v:
return i, true
// if none of the previous cases is matched, proceed to the next node.
default:
n = n.next
}
}
// return 0 and false to notify there is no index matching the value.
return 0, false
}
Conclusion
There are many more behaviors that can be part of a singly linked list, such as adding or deleting a node to a given position, as well as finding a value at a given index etc.
The singly linked list is a powerful and robust data structure, which makes perfect sense in use cases where:
- adding or deleting nodes to be efficient and can be done in front
- there is no need for access nodes in the middle of the sequence
- the number of items needs to contain in unknown
It is often used as a core data structure to implement queues and stacks, even if there are more efficient ways to implement those.
Last but not least a recap of the time complexity of the operations a singly linked list can support:
| Operation | Time complexity |
|---|---|
| AddFront | O(1) |
| AddBack | O(n) |
| DeleteFront | O(1) |
| DeleteBack | O(n) |
| Find | O(n) |
| Index | O(n) |